ROVINNÁ GEOMETRIE:

BOD - je určen souřadnicemi, zjednodušeně můžeme říci, že je to určení místa, polohy, . . .

Rovina- je to neomezená rovná plocha, můžeme si jí představit jako vršek lavice, podlaha ve třídě, střecha paneláku(cokoliv plochého když se podíváme ze shora). Je určena třemi různými body.

PŘÍMKA - je to nekonečně dlouhá čára.

POLOPŘÍMKA - je to přímka ohraničená z jedné strany.

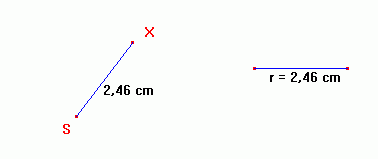
ÚSEČKA - je to přímka ohraničená dvěma body.

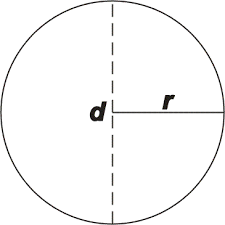
KRUH - je to nakreslené kolo i s vnitřkem, má střed -S, poloměr -r a průměr -d

KRUŽNICE - je to nakreslené kolo bez vnitřku, má vždy stejnou vzdálenost od středu.

KRUŽNICE OPSANÁ - kružnice prochází všemi vrcholy trojúhlníka a střed kružnice je v průsečíku os stran.

KRUŽNICE VEPSANÁ - kružnice se dotýká všech stran trojúhelníka a střed kružnice je v průsečíku os vnitřních úhlů.

VÝŠKA - je úsečka vedená vrcholem na protější stranu;každý trojúhelník má 3 výšky;vytvoříme jí pomocí trojúhelníku s ryskou

             (přiložíme rysku na dannou stranu a opačný vrchol-spojovací čára je výška);spojením všech výšek vznikne pata výšky.

TĚŽNICE - je úsečka vedená středem strany a protilehlý vrchol trojúhelníku. Každý trojúhelník má tři těžnice. Těžnice se

                  protínají v jednom bodě, který se nazývá těžiště.

VĚTY O SHODNOSTI TROJÚHELNÍKŮ - dva trojúhelníky ABC a A´B´C´ se nazývají shodné trojúhelníky, jestliže je lze přemístit

                                                                          tak, že se úplně kryjí; věty o shodnosti jsou:

                                        1. "sss"-shodují-li se dva trojúhelníky ve všech třech sobě odpovídajících stranách, pak jsou shodné.;

                                        2. "sus" -shodují-li se dva trojúhelníky ve dvou stranách a úhlu jimi sevřeným, jsou shodné;

                                         3. "usu" -shodují-li se dva trojúhelníky v jedné straně a v obou úhlech k ní přilehlých, jsou shodné;

OBDÉLNÍK - skládá se ze čtyř stran a čtyř úhlů (dohromady 360 stupňů) protilehlé strany jsou stejně dlouhé.

ČTVEREC - skládá se ze čtyř stran a všechny jsou stejně dlouhé.

ROVNOBĚŽKY - jsou to dvě přímky, které se nikdy neprotnou.

KOLMICE - jsou to přímky, které spolu svírají úhel 90 stupňů.

JEDNOTKY A DÉLKY - každá veličina (popis něčeho) má svou jednotku; v matematice využíváme základní veličiny:

                                        délka - mm, cm, dm, m, km; značíme d

                                        obsah - to samé jako délka, ale čtvereční neboli na druhou; značíme S-vždy násobíme dvě délky

                                        váha - g, dkg, kg, tuna; značíme m (hmotnost)

                                        objem - stejně jako dělka, ale krychlové (na třetí), značíme V-vždy násobíme tři délky; 1dm krychlový=1litr

                                        čas - sekunda, minuta, hodina, den, týden, měsíc, rok; značíme t

                                        rychlost - m/s nebo km/h; značíme v; rychlost auta-potřebujeme znát vzdálenost a čas

PŘEVODY - 1m=10dm=100cm=1000mm; 1mm=0,1cm=0,01dm=0,001m; 1km = 1000m

                     čtvereční se posouvají o dvě místa - 1m=100dm=10000cm=1 000 000mm; krychlové o tři místa

OBSAH A OBVOD - obsah je plocha, která je ve vnitř (vymalování pokoje), obvod co je okolo (stavění plotu okolo zahrady).

                               obsah jsme si již řekli, že vychází ve čtverečních jednotkách (na druhou)=musíme násobit dvě velikosti.

                                obvod vychází v základní jednotce metr = pouze sčítáme délky.

ČTVEREC - S= a ° a (strana na druhou) o=a+a+a+a=4 ° a

OBDÉLNÍK - S= a ° b (strana ° druhá strana) o= a+b+c+d (strany a,c jsou stejné + strany b,d jsou také stejné)=2a+2b=2(a+b).

PROSTOROVÁ GEOMETRIE:

POVRCH - je obsah všech stěn v tělese (natření celé třídy), značí se S a vychází v jednotkách čtverečních

OBJEM - určuje velikost (množství) kolik se vejde vody (vzduchu) do tělesa, značí se V a vychází v jednotkách krychlových, 1dm krychl. = 1 litr

KRYCHLE - se skládá z šesti čtverců, má tedy šest stěn (krabice), Povrch se vypočítá S=6°a°a Objem V = a°a°a

KVÁDR -  se skládá z šesti obdélníků (každé dva protilehlé obdelníky jsou stejné, má tedy šest stěn (třída, pokoj),

                 Povrch se vypočítá S=2°(a°b + a°c + b°c)  Objem V = a°b°c

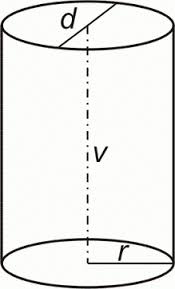
VÁLEC - se skládá z obdélníku či čtverce a dvou kruhů (trubka či roura)

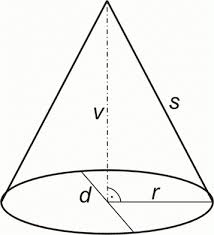
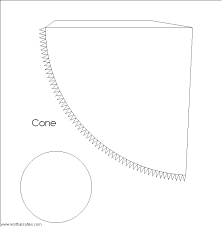
KUŽEL

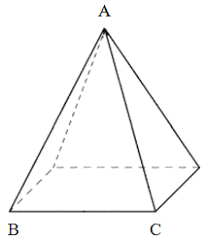
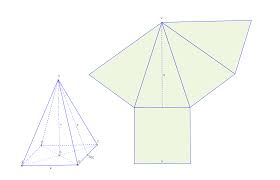
JEHLAN - se skládá z podstavy (na čem stojí-obdélník, čtverec, mnohoúhelník) a trojůhelníků

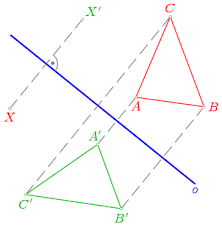
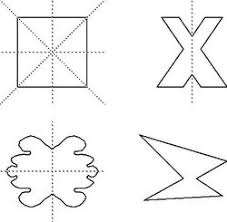
OSOVÁ SOUMĚRNOST - je to přenášení útvarů přes osu; přenáším stejnou vzdálenost a pod úhlem 90° (kolmicí); obrázek bude zrcadlově (osa je jako

                                            místo kde přeložením papír a obrázek se mi obtiskne)

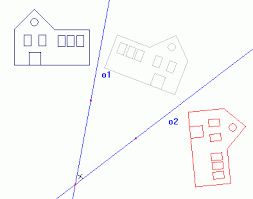
STŘEDOVÁ SOUMĚRNOST - je přenášení vzoru (obrázku) přes jediný bod (střed) a nanášení stejných vzdáleností

DESETINNÁ ČÍSLA - desetinné číslo má desetinou čárku (7,33), čteme ho celým číslem a podle poslední pozice (nenulové) za desetinou čárkou

                                      př. 1, 308 - jedna celá a třistaosm tisícin; 2, 0058 - dvě celé padesátosm desetitisícin; 0,02 - žádná celá dvě setiny

 ,   ,    ,

POROVNÁVÁNÍ DESETINNÝCH ČÍSEL - čísla porovnáváme (zda je větší či menší) podle velikosti v daném řádu

,je větší než,

--------------------------------             ------------------------------------  ------------------------------------               --- stejné                                    ----------------------------------------     ------------------------------------------  ----------------------------------

SČÍTÁNÍ A ODČÍTÁNÍ DESETINÝCH ČÍSEL -  sčítají a odčítají se stejně jako čísla přirozená (bez desetinné čárky) jen musíme sčítat spolu

                                                                                  stejné řády (setiny se setinama; tisíciny s tisícinami, jednotky s jednotkami) 

                                                  př.               ,        ,

                                                  +  ,     - ,

                                                                          --------------------------------------------------------------------------------------------------------                     ------------------------------------------------------------------------------------------------

                     ,       ,

NÁSOBENÍ DESETINNÝCH ČÍSEL - násobí se stejně jako čísla přirozená (bez desetinné čárky), jen ve výsledku odsuneme desetinou čárku

                                                                  do leva o tolik míst kolik je desetinných míst v příkladě.    

                                                                 př. 1,21 ° 4 = 121 ° 4 = 484 a nní posuneme o dvě desetinná místa z prava do leva = 4, 84 

DĚLENÍ DESETINNÝCH ČÍSEL - 1) máme-li desetin. čárku v čísle které dělíme, tak dělíme stejně jako s čísly přirozenými (bez desetinné

                                                                čárky) pouze až při dělení dojdeme k desetinné čárce, čárku opíšeme do výsledku a v dělení pokračujeme

                                                              př 8, 31: 3= 2,77

                                                                     2 (nyní bych opsal deset. čárku, takže jí napíši do výsledku a pokračuji opsáním dalšího čísla v pořadí)

                                                                     23

                                                                       21 zbytek 0

                                                          2) desetinou čárku máme v dělitely - musíme vynásobit ( 10, 100, 1000, ...) příklad (posunout desetinnou

                                                                                                                         čárku) o tolik aby v dělitely bylo přirozené číslo (bez desetinné čárky)

                                                              př. 159 : 12,24 = ° 100 (musíme posunout o dvě desetinná místa - vynásbit stem)

                                                                     15900 : 1224 = již počítáme

                                                          3) číslo které dělíme je menší než dělitel - do výsledku napíšeme nulu a desetinou čárku; do čísla co dělíme

                                                                                                                         připíšeme nulu nebo posuneme desetinou čárku do prava o jedno místo.

                                                                př. 5 : 8 = 0, 625

                                                                       50

                                                                        20

                                                                          40

DĚLITELNOST - pravidla jak poznáme, že číslo je dělitelné právě tímto číslem:

         dělitelné dvěmi: na konci čísla je sudé číslo (0,3,4,6,8,) př. 134;111118;06

         dělitelné třemi: jednotlivá čísla sečteme a výsledek je dělitelný třemi. př.141=1+4+1=6/6 lze;12345=1+2+3+4+5=15/3 lze

        dělitelné čtyřmi: pokud poslední dvojčíslí jě dělitelné čtyřmi. př. 612, 1048

        dělitelnost pěti: na posledním místě je 0 nebo 5. př. 100, 2345

        dělitelnost šesti: je-li dělitelné dvěmi i třemi

         dělitelnost sedmi: že se první až posldní číslice od zadu vynásobí postupně čísly (periodicky se opakujícími): 1, 3, 2, 6, 4, 5

                                    př. 138309241 : 1*1+4*3+2*2+9*6+0*4+3*5+8*1+3*3+1*2=105 (1*5+3*0+2*1=7, číslo dělitelné 7)

         dělitelnost osmi: je-li poslední trojčíslý dělitelné osmi. př. 12016, 6064

          dělitelsnost devíti: jednotlivá čísla sečteme a výsledek je dělitelný devíti. př. 15786=1+5+7+8+6=27/9 lze

          dělitelnost desíti: končí-li číslo na nulu. př. 100, 1230, 1836400

 ARITMETICKÝ PRŮMĚR - se vypočítá sečtením všech položek a vydělením počtem položek. př. 5 a 7;(5+7)/2=12/2=6

PŘEVOD ZLOMKU NA CELKY - vydělíme čitatele jmenovatelem - vyjde celek a zbytek napíšeme do čitatele. př.15/8=1a7/8

PRVOČÍSLO - číslokteré je dělitelné pouze číslem jedna a sebou samým;př.3, 5, 7, 11, 13, 17, 22, 31;pozor číslo 1 není prvočíslo.

ROZKLAD ČÍSEL NA PRVOČÍSLA - danné číslo rozložíme na co nejmenší násobky - prvočísla. př. 27=9 ° 3=3°3°3

NEJMENŠÍ SPOLEČNÝ NÁSOBEK - nalézneme tak, že každé z čísel je rozložíme na součin prvočísel a yvpíšme čísla, která se

                                                                   vyskytují alespoň v jednom rozkladu; př. čísla: 15 a 20

 ABSOLUTNÍ HODNOTA - je to závorka / / která převádí záporné čísla na kladné (z mínus 3 se stane plus 3). př. /-3+5-8/=/-6/=6

PROCENTA % - vyjadřují část celku. Vypočítání procent z čísel: část celku / celek ° 100 = %; 2 ze 4 = 2/4°100=50%

                                                     Vypočítání části celku z procent: celek / 100 ° procenta = část celku; 50% ze 4 = 4/100°50=2

                                        Vypočítání celku z procent a části celku: 100% / počet procent °část celku = celek; 2 je 50% = 100/50°2=4

JEDNODUCHÉ ROVNICE - rovnice poznáme tak, že má rovnítko (=) takže má pravou stranu (před rovnítkem) a levou stranu (za

                                                  rovnítkem). Nejdůležitější je si uvědomit, že obě strany se musejí rovnat (musí být stejný výsledek).

                                                  př. c - 230 = 50; pokavaď je na pravé straně 50, tak na levé musí vyjít také 50. Nyní je příklad již

                                                   jednoduchý, stačí najít jen číslo za c aby vyšlo 50. Což je 280 - 230 = 50

GEOMETRICKÝ SLOVNÍK:

1. BOD, VRCHOL  se značí velkým tiskacím písmenem
2. ÚSEČKA, STRANA, KRUŽNICE se značí malými psacími písmeny
3. ÚHEL se značí řeckými písmeny
4. POLOMĚR se značí r
5. STŘED RUHU se značí S
6. VELIKOST ÚSEČKY se značí /AB/=  cm
7. VELIKOST ÚHLU se značí /AVB/= °
8. PRŮNIK se značí ∩ 
9. NÁLEŽÍ se značí (obsahuje) ∈

KONSTRUKCE GEOMETRICKÝCH ÚTVARŮ:

• NÁČRT - zakreslíme od ruky veškeré informace, které známe ze zadání
• ZÁPIS - zapisujeme podle geometrického slovníku co budeme dělat
• KONSTRUKCE - vytvoříme daný útvar
• POČET ŘEŠENÍ - uvedeme počet řešení

ZÁPIS PODLE VĚT O SHODNOSTI TROJÚHELNÍKU (jaké údaje máme):

ZAPÍŠEME ČÍSLOVKU (pořadí) POTÉ CO CHCEME VYTVOŘIT, STŘEDNÍK A POTÉ JAK TO VYTVOŘÍME!!!

ZNÁME STRANU, STRANU, STRANU (sss):

1. zapíšeme stranu kterou budeme konstruovat, středník a zapíšeme kolik úsečka měří
2. zapíšeme název kružnice, středník a napíšeme název kružnice, závorku a do ní bod do kterého zabodneme kružítko, středník a poloměr=velikost strany
3. zapíšeme název druhé kružnice, středník a napíšeme název kružnice, závorku a do ní bod do kterého zabodneme kružítko, středník a poloměr=velikost strany
4. zapíšeme vrchol, který chceme vytvořit, středník a název vrcholu, který náleží průniku obou kružnic
5. vytvořímě trojúhelník ABC

UKÁZKA:

1. c;/AB/= cm
2. k; k(A;r= cm)
3. l; l(B; r= cm)
4. C; C∈k∩l
5. trojúhelník ABC