V TÉTO SEKCI NALEZNETE ZJEDNODUŠENÝ VÝKLAD LÁTKY

Vrhneme se na nejzákladnější pravidla matematiky (pro základní školy) bez kterých to NEJDE=o((((                                      

 ČÍSLO URČUJE POČET ČI MNOŽSTVÍ

 číselná SOUSTAVA - MĚJME ČÍSLO 1234567,89 ČÁRCE MEZI ČÍSLI ŘÍKÁME DESETINNÁ A ROZDĚLUJE ČÍSLO NA JEDNOTKY A DESETINY

V ČÍSLE 1234567,89 URČUJE číslo 7-JEDNOTKY (první pozice před desetinou čárkou), číslo 6-DESÍTKY (druhá pozice před desetinou čárkou), číslo 5-STOVKY (třetí pozice před desetinou čárkou), číslo 4-TISÍCE (čtvrtá pozice před desetinou čárkou), číslo 3-DESETI TISÍCE (pátá pozice před desetinou čárkou), číslo 2-STA TISÍCE (šestá pozice před desetinou čárkou), číslo 1-MILIONY ( sedmá pozice před desetinou čárkou), číslo 8-DESETINY (první pozice po desetiné čárce), číslo 9- SETINY (druhá pozice po desetiné čárkce)

                                                                     

PŘIROZENÁ ČÍSLA - značíme je N a patří do nich čísla kladná = od 1 - nekonečna(1;2;3;4;5;...) = nula do nich nepatří

                                  Můžeme je libovolně sčítat: 5 + 3 = 3 + 5 (nezáleží na pořadí)

                                  Múžeme je libovolně násobit: 8 ° 3 = 3 ° 8 (nezáleží na pořadí)

                                Můžeme libovolně přehazovat závorky u sčítání: (3 + 5) + 1 = 3 + (5 + 1) 

                                  Můžeme libovolně přehazovat závorky u násobení: (3 ° 5) ° 1 = 3 ° (5 ° 1)

                                  Násobíme-li cokoliv jedničkou vyjde to samé číslo: 8 ° 1 = 8

                                  Platí roznásobení závorek: 3 ° (5 + 3) = 3 ° 5 + 3 ° 3 (tzv. každý z každým)

CELÁ ČÍSLA - značíme je Z a patří do nich čísla kladná i záporná a nula (- ...;-2;-1;0;1;2;...)

                      Platí stejná pravidla jako s přirozenými čísly a navíc:

                       Přičteme-li nulu ke kterémukoliv číslu, vyjde stejné číslo (přičítám nic): 5 + 0 = 5

                      Vynásobíme-li jakékoliv číslo nulou, vyjde nula: 7 ° 0 = 0

RACIONÁLNÍ ČÍSLA - značíme je Q a patří do nich zlomky (dělení)

                                  Platí pro ně stejná pravidla jako s celými čísly a navíc:

                                   Dělíme - li nulu jakýmkoliv číslem, vyjde nám vždy nula: 0 / 3 = 0

                                  !!!!DĚLIT NULOU NELZE!!!!  5 / 0 = NELZE (NEMŮŽEME NAPSAT 0)        

REÁLNÁ ČÍLA - značíme je R a jsou to všechna čísla se kterými se na základní škole setkáme    

                          Platí pro ně stejná pravidla jako pro čísla racionální a navíc:

                          Násobíme-li stejná čísla s různou mocninou, tak číslo opíšeme a mocniny sečteme:

                                                            5 na třetí ° 5 na druhou = 5 na pátou

                         Dělíme-li stejná čísla s různou mocninou, tak číslo opíšeme a mocniny odečteme:

                                                            5 na třetí / 5 na druhou = 5 na prvou

                          Cokoliv na nultou je jedna: 8 na nultou = 1

                          Cokoliv na prvou je to číslo: 8 na prvou = 8

                                                         

ZAOKROUHLOVÁNÍ - Při zaokrouhlování se řídíme nejbližším číslem nižšího řádu, což znamená, když zaokrouhlujeme na desítky, koukám na jednotky, setiny  ¨

                                                          koukám na desítky, atd.

 ZAOKROUHLUJEME DOLU:0,1,2,3,4 - číslo ponechám a za něj napíšu nuly

zaokrouhlujeme nahoru: 5, 6, 7, 8, 9 - k číslu přičtu jedničku a za něj napíšu nuly

číslo 9472 zaokrouklete na, desítky, stovky a tisíc.

na desítky: vždy koukám na nižší řád což jsou jednotky, takže u nás je to dvojka a ta se zaokrouhluje dolu = 9470

Na stovky: vždy koukám na nižší řád což jsou desítky, takže u nás je to sedmička a ta se zaokrouhluje nahoru = 9500

Na tisíce: vždy koukám na nižší řád což jsou stovky, takže u nás je to čtyřka a ta se zaokrouhluje dolu = 9000

 

SČÍTÁNÍ - Sčítání nedělá velké problémy nikomu, takže v rychlosti. Poznáme ho dle znaménka plus (+); Koupím máslo, rohlík a chléb=kolik

                      jsem koupil věcí???                                                     1+1+1=3   + znamená, že něco mám,přidávám

                                                  + =

ODČÍTÁNÍ - Odčítání by též nemělo dělat problém, proto se ihned podíváme na odčítání do záporných čísel. Odčítání má znaménko mínus (-); Mám 30 korun a nákup

                                    stojí 50 korun, kolik korun mi chybí???                                        30 - 50=-20   - znamená, že něco beru, dlužim            

                                            - =

 

PRAVIDLO PRO SČÍTÁNÍ A ODČÍTÁNÍ

   - Mám-li dvě stejná znaménka, tak znaménko opíši a čísla sečtu +5+3=+8 (plusy); -2-7= -9 (mínusy)

     - Mám-li dvě různá znaménka, tak opíši znaménko u většího čísla a menší číslo od většího odečtu

                                                                                                                          -3+5=+2 (číslo pět je větší než tři a je u něj plus, takže opíši plus a poté jen 5-3=2)

                                                                                                         -7+5=-2 (číslo sedm je větěí než číslo pět a je u něj mínus, takže opíši mínus a poté jen 7-5=2)

NÁSOBENÍ A DĚLENÍ - Násobení znamená - přinesu sedm brambor;  mám sedmkrát po jedné bramboře 7 krát 1.

                                                                    - Dělení znamená - Zbylo mi dvanact korun a mám je rozDĚLIT mezi tři kamarády; 12 / 3

Zde je nejdůležitější si uvědomit tyto vztahy:

1. + krát + = +               5 KRÁT 3 = +15      krát   = 

2. - krát - = +                 -3 KRÁT -9 = + 27    krát    = 

3. - krát + = -                 -6 KRÁT 2 = -12      krát     = 

4. + krát - = -                 8 KRÁT -5 = -40     krát    = 

 

Dvě stejná znaménka dají vždy plus a dvě různá dají mínus.

ZÁVORKY a PŘEDNOSTI ZNAMÉNEK - máme různé druhy závorek [<()>], ale nejdůležitější je nejdříve vypočítat vnitřní a později pokračovat s vnějšími.

  přednosti znamének též není žádná věda: nejdříve mocníme a odmocňujeme, poté násobíme a dělíme a nakonec sčítáme a odčítáme.

SHRNUTÍ - nejdříve vypočítáme závorky (pokavaď to lze)-dokud se všech nezbavíme; poté mocníme,odmocňujeme; pak násobíme, dělíme a nakonec sčítáme,odčítáme.

5°[7-<3+ (4/2) - 2>³+ 1}+ 1= 5°<7-(3 + 2 -2)³ + 1> +1= 5 ° (7-3³+1) +1= 5 ° (7-27+1) +1= 5° (-19) + 1= -95 +1= -94

nejdříve vypočteme vnitřní závorku (4/2) a vždy pokud mohu co je v závorce - základní pravidlo=vždy se zbavovat závorek; poté mají přednost mocniny (3)³;násobení;sčítání a odčítání.                                          

                                                                 =

ROZNÁSOBENÍ ZÁVOREK (MNOHOČLENŮ) - 1) Pokud roznásobujeme závorku mínusem, jen změníme znaménka v závorce:

                                                                                            př. -(x + 3 - y) = - x - 3 + y

   2) Pokud roznásobujeme závorku kladným číslem či neznámou, každý člen v závorce vynásobíme číslem před závorkou (znaménka opisujeme):

                                                                př. 3 (5 + x) = 3 ° 5 + 3 ° x = 15 + 3x;               a (7 - y + x) = a ° 7 - a ° y + a ° x = 7a - ay + ax

        3) Pokud roznásobujeme závorku záporným číslem či členem, každý člen v závorce vynásobíme číslem před závorkou (znaménka změníme):

                                                               př. -c (3 - x) = -c ° 3 - c ° (-x) = -3c + 3x               -2 (-5 + x - q) = -2 ° (-5) -2 ° x - 2 ° (-q) = 10 - 2x + 2q 

  4) Roznásobení mnohočlenu mnohočlenem:

                                                              a) násobíme prvním členem prvního mnohočlenu první člen druhého členu dle pravidel (1-3)

                                                              b) násobíme prvním členem prvního mnohočlenudruhý člen druhého členu dle pravidel (1-3) 

                                                              c) neustále opakujem až k poslednímu členu druhého mnohočlenu

                                                              d) násobíme druhým členem prvního mnohočlenu první člen druhého členu dle pravidel (1-3)

                                                              e) násobíme druhým členem prvního mnohočlenu další člen druhého členu dle pravidel (1-3)

                                                               f) dále až do posledního členu druhého mnohočlenu

                                        g) násobíme dalším členem prvního mnohočlenu první člen druhého členu dle pravidel (1-3) a postupujeme dle bodů (a-f)

                                                              h) sečteme členy co můžeme sečíst a seřadíme dle velikosti mocnin a neznámých dle abecedy

                  př. (3x + 7) ° (-5 + y)= 3x ° (-5) {a] + 3x ° y {b] + 7 ° (-5) {d] + 7 ° y {e] = -15x + 3xy - 35 + 7y {a-f] = -15x + 3xy + 7y - 35 {h]

DĚLĚNÍ MNOHOČLENU : Dělení se provádí stejně jako když dělíme dvě čísla se zbytkem

                                               a) neznámou s nevyšší mocninou vydělíme dělitelem a zapíšeme do výsledku

                                                b) neznámou s druhou nejvyšší mocninou vydělíme dělitelem a zapíšeme do výsledku

                                                c) takto postupujeme dokud můžeme dělit mnohočlen dělitelem

                                                d) zbytek napíšeme do výsledku a vydělíme dělitelem

                                                př.   ( 4(x) na druhou + 8x - 50 ) : 4x = x (a) + 2 (b) - 50/4x (d)

 

ZLOMKY - Máš pizzu na 8 dílů? Máš o polovinu úkolu špatně? Třetina třídy je nemocná? Snědl jsi čtvrtinu melouna?= toto všechno jsou zlomky

                                                             

ve zlomku je čitatel - to nahoře-označuje kolik dílů je vyplněných; zlomková čára (můžeme říci, že je to i děleno); to dole je jmenovatel-označuje na kolik dílků se zlomek dělí.  2/4 - dvě čtvrtiny; dvě děleno čtyřmi - výsledek je stejný!!!!

PŘEVOD ZLOMKU NA CELKY - čitatel / jmenovatel= počet celků a zbytek napíšeme do čitatele, jmenovatele opíšem.

                                                           11/4=11:4=2(zbytek3)=2 celky a 3/4 = dvě pizzy a ze třetí jeden kousek chybí

PŘEVOD CELKŮ NA ZLOMKY -celek ° jmenovatel + čitatel = výsledný čitatel a jmenovatele opíšu. 2 celky a 3/4= 2 ° 4 + 3 = 11/4

SČÍTÁNÍ A ODČÍTÁNÍ ZLOMKŮ - najdeme společného jmenovatele (vezmeme toho většího jmenovatele a postupně ho násobíme dokud nepůjde vydělit druhým jmenovatelem); společnýho jmenovatele vydělíme prvním jmenovatelem a vynásobíme prním čitatelem; opíšeme znaménko a to samé z druhým zlomkem (vezmeme společného jmenovatele a vydělíme druhým jmenovatelem a vynásobíme druhým čitatelem); poté již jen vypočítáme.

3/4 - 8/3 = (3°3 - 4°8) / 12 = (9 - 32) / 12 = - 23 / 12  

společný jmenovatel 4 a 3 - vezmeme násobky 4 (je větší číslo) a pokoušíme zda je dělitelné 3 (ten druhý menší jmenovatel);4/3-neumíme;další násobek čtyřky je osmička- 8/3-neumíme, další násobek čtyřky je dvanáctka-12/3 umíme a je to čtyřka; společný jmenovatel 4 a 3 je dvanáctka

Koukneme se na obrázek s máslem      1/2 + 1/2 = (1+1)/2 = 2/2 = 1 = celek

ROZŠIŘOVÁNÍ ZLOMKŮ - zlomky rozšíříme vynásobením jmenovatele a čitatele stejným číslem

                                                př. 8/3 rozšířím čtyřmi = 8 ° 4 / 3 ° 4 = 32/12

KRÁCENÍ ZLOMKŮ - zlomky krátíme nalezením takového čísla, že jím jde vydělit jmenovatel i čitatel

                                                př. 40/16 = 40 i 16 lze vydělit osmi = 40 : 8 / 16 : 8 = 5/2

ROVNOST ZLOMKŮ - rovnost nastane tehdy, pokud při zkrácení (či rozšíření) zlomku nám vyjde požadovaný druhý zlomek

                                               př. 2/3 =???=16/24  ; 16/24 jde zkrátit osmi = 16:8 / 24:8 = 2/3; takže jsou ai rovny 2/3=2/3

NÁSOBENÍ ZLOMKŮ - zlomky se násobí vynásobením čitatelů=výsledek napíši do výsledného čitatele a vynásobení

                                                             jmenovatelů=výsledek napíši do výsledného jmenovatele. Použiji křížové pravidlo (zkrátím 1.čitatele z

                                                            2.jmenovatelem a 1.jmenovatelem z druhým čitatelem = křížem krátím) - pokud lze a pak jen vynásobím 

                                                            čitatele a jmenovatele.       př. 3/16 ° 24/9 = 3 a 9 jde zkrátit třemi a 16 a 24 jde zkrátit osmi

                                                                                                                                  = 1/2 ° 3/3 = 1 ° 3 / 2 ° 3 = 3 / 6 to jde ještě zkrátit třemi = 1/2

DĚLENÍ ZLOMKŮ - zlomky se dělí pomocí 1)přehozením čitatele se jmenovatelem ve druhém zlomku 2) pak se zlomky mezi sebou VYNÁSOBÍ

                                                                 PŘ.   8/3 : 16/6 = 8/3 ° 5/16= lze krátit 1.čitatele se 2.jmenovatelem osmi = 1/3 ° 5/2 = 1 ° 5 / 3 °2 = 5/6

VÝRAZY - asi největší problém na základní škole, takže půjdeme polopatě =o)

Výraz poznáme tak, že je tam nějaká neznámá (písmenko) a není to rovnice (bez rovnítka -nevychází nám výsledek).

Ukázka výrazu: 5a+x-3z   . . . máme tam 3 neznámé (písmenka a;x;z), není tam rovnítko-není to rovnice

Co ty neznámé (písmenka) znamenají??? - cokoliv si představite; například auto, pivo, zub, rtěnku

řekneme se tedy, že a je autobus; x je ponožka; z je holub z nosu ------takže příklad můžeme říci, že zní takto:

5 AUTOBUSŮ +  PONOŽKA - 3 HOLUBY Z NOSU je . . .

Už možná víme jak výraz poznáme, ale co s ním budeme dělat???

Můžeme za neznámé dosadit čísla a vypočítat (což nalezneme v zadání příkladu) - např a=1;x=2;z=0           5°1+1°2-3°0=5+2-0=7 Nezapomínáme na přednosti, jak je popsáno o kapitolu výše.

Nebo ho jen budeme upravovat, což si můžete představit že místo toho abyste říkal, že jdete koupit: rohlík, rohlík, rohlík, rohlík, rohlík, máslo, colu, colu, colu ŘEKNETE 5 rohlíků, máslo a 3 coly.

VE výrazech upravujeme: sčítáme a odčítáme; násobíme a dělíme; mocníme a odmocňujeme

SČÍTÁNÍ A ODČÍTÁNÍ: 5x + 3y - 3x -2y + z      řekneme si, že x je noha; y je pes a z je chlup, takže kolik je 5 noh+3psy-3hohy-2psy+chlup???

2x + y + z                                                               asi zvládneme, že jsou to 2 nohy, jeden pes a jeden chlup

MALÁ UKÁZKA:

+   + +        +   + ++ =

 2+ 3 + 3

TAKŽE POKUĎ SČÍTÁME ČI ODEČÍTÁME, TAK JEN STEJNÉ VĚCI . . . PŘECI NEHET + SOPKA NIC NENI, TAK NEMŮŽEME POČÍTAT DVĚ RŮZNÉ VĚCI DOHROMADY . . . .   X + Y SE NEDÁ SČÍTAT    +  = NELZE

NÁSOBENÍ A DĚLENÍ: 5x ° 4y ° 3f     u násobení a dělení si vždy představte něco k pití za neznámé; x je voda; y je cola; f je čaj

při násobení a dělení všechny tyto tekutiny sléváme dohromady a vytváříme nově drinky.

5x ° 4y=5°4 xy....Takže slejeme pěti vody s čtyřmi coly a třemi čaji což z toho vznikne něco nového - např. pět vod s čtyřmi coly je5 ° 4 COLVODA a

5°4 xy ° 3f= 5°4°3 xyf....       poté do toho nalejeme ještě zbylý tři čaje; což bude 5°4°3 COLVODAČA; poté jen čísla vynásobíme = 60COLVODAČA

X°Y = xy

  °=

VZORCE PRO VÝRAZY (ÚPRAVY) - máme pět základních postupů:

                          1. vzorec: (A + B) na druhou = (A + B) ° (A + B) = A na druhou + 2AB + B na druhou

   Postup: umocníme první člen na druhou; vynásobíme dvěma první a druhý člen; umocníme na druhou druhý člen

                                  př.(x + 3) na druhou = x na druhou + 2°x°3 + 3 na druhou = x na druhou + 6x + 9

   Postup: odmocníme první člen a zapíšeme do závorky; odmocníme poslední člen a zapíšeme do závorky; vynásobíme

                dvěma první a druhý člen v závorce a musí nám vyjít prostřední člen; umocníme celou závorku na druhou

                                  př. 4(x) na druhou + 16x + 16 = (2x + 4) na druhou

                          2. vzorec: (A - B) na druhou = (A - B) ° (A - B) = A na druhou - 2AB + B na druhou

  Postup: to samé jak u + jen za prvním členem a v závorce je mínus

                          3. vzorec: (A + B) ° (A - B) = A na druhou - B na druhou

  Postup: máme dva členy umocněné na druhou; mezi nima odčítání; odmocním první a druhý člen a zapíšu do závorek

                                  př. 16 - 9(x) na druhou = (4 - 3x) ° (4 + 3x)   . . . . . . . . . 9(x) na druhou = 3x ° 3x; 16= 4 ° 4 

                           4. vytýkání - pokud se nějaké číslo či neznámá opakuje v každém členu, mohu jí vytknout před závorku

                                  př. 3x - 9 = 3 (x - 3)

                           5. rozklad kvadratické rovnice na součin

 Postup: Toto pravidlo platí pokud člen na druhou má násobek jedna = 1°(x) na druhou. Vemu poslední člen a rozložim

                ho na násobení; rozložené čísla sečtu a musí mi vyjít prostřední člen; rozložená čísla, která tomuto pravidlu

               vyhovují zapíšu do závorek s neznámou.

                                př. 1x na druhou + 6x - 27; -27 = (-1°27), (1°-27), (-3°9), (3°-9); když čísla sečtu má vyjít +6 =

                                                                                                        (-1 + 27), (1 - 27), (3 - 9) nesouhlasí,(-3+9)=6;

                                                                                           nyní jen napíšu do závorek (x+...)°(x+...) = (x-3)°(x+9)  

                                        x na druhou + 6x - 27 = (x - 3) ° ( x + 9)

 

GEOMETRIE:

BOD - je určen souřadnicemi, zjednodušeně můžeme říci, že je to určení místa, polohy, . . .

Rovina- je to neomezená rovná plocha, můžeme si jí představit jako vršek lavice, podlaha ve třídě, střecha paneláku(cokoliv plochého když se podíváme ze shora). Je určena třemi různými body.

PŘÍMKA - je to nekonečně dlouhá čára.

POLOPŘÍMKA - je to přímka ohraničená z jedné strany.

ÚSEČKA - je to přímka ohraničená dvěma body.

KRUH - je to nakreslené kolo i s vnitřkem, má střed -S, poloměr -R a průměr -D,

KRUŽNICE - je to nakreslené kolo bez vnitřku, má vždy stejnou vzdálenost od středu.

TROJÚHELNÍK - skládá se ze tří stran a třech úhlů(alfa, beta, gama)=dohromady mají 180 stupňů; trjúhelníková nerovnost

                              znamená, že když sečtu jakékoliv dvě strany musí být součet větší než třetí strana a + b > c, a + c > b, b + c > a;

                              trojúhelníky máme ROVNOSTRANNÝ-všechny strany stejně dlouhé (každý úhel je 60stup);ROVNORAMENNÝ-

                              dvě strany jsou stejně dlouhé (dva úhly jsou shodné);OSTROÚHLÝ – všechny vnitřní úhly jsou ostré;

                              PRAVOÚHLÝ – jeden vnitřní úhel je pravý, zbývající dva jsou ostré;TUPOÚHLÝ – jeden vnitřní úhel je tupý,

                              zbývající dva jsou ostré.

KRUŽNICE OPSANÁ - kružnice prochází všemi vrcholy trojúhlníka a střed kružnice je v průsečíku os stran.

KRUŽNICE VEPSANÁ - kružnice se dotýká všech stran trojúhelníka a střed kružnice je v průsečíku os vnitřních úhlů.

VÝŠKA - je úsečka vedená vrcholem na protější stranu;každý trojúhelník má 3 výšky;vytvoříme jí pomocí trojúhelníku s ryskou

             (přiložíme rysku na dannou stranu a opačný vrchol-spojovací čára je výška);spojením všech výšek vznikne pata výšky.

TĚŽNICE - je úsečka vedená středem strany a protilehlý vrchol trojúhelníku. Každý trojúhelník má tři těžnice. Těžnice se

                  protínají v jednom bodě, který se nazývá těžiště.

VĚTY O SHODNOSTI TROJÚHELNÍKŮ - dva trojúhelníky ABC a A´B´C´ se nazývají shodné trojúhelníky, jestliže je lze přemístit

                                                                          tak, že se úplně kryjí; věty o shodnosti jsou:

                                        1. "sss"-shodují-li se dva trojúhelníky ve všech třech sobě odpovídajících stranách, pak jsou shodné.;

                                        2. "sus" -shodují-li se dva trojúhelníky ve dvou stranách a úhlu jimi sevřeným, jsou shodné;

                                         3. "usu" -shodují-li se dva trojúhelníky v jedné straně a v obou úhlech k ní přilehlých, jsou shodné;

OBDÉLNÍK - skládá se ze čtyř stran a čtyř úhlů (dohromady 360 stupňů) protilehlé strany jsou stejně dlouhé.

ČTVEREC - skládá se ze čtyř stran a všechny jsou stejně dlouhé.

ROVNOBĚŽKY - jsou to dvě přímky, které se nikdy neprotnou.

KOLMICE - jsou to přímky, které spolu svírají úhel 90 stupňů.

JEDNOTKY A DÉLKY - každá veličina (popis něčeho) má svou jednotku; v matematice využíváme základní veličiny:

                                        délka - mm, cm, dm, m, km; značíme d

                                        obsah - to samé jako délka, ale čtvereční neboli na druhou; značíme S-vždy násobíme dvě délky

                                        váha - g, dkg, kg, tuna; značíme m (hmotnost)

                                        objem - stejně jako dělka, ale krychlové (na třetí), značíme V-vždy násobíme tři délky; 1dm krychlový=1litr

                                        čas - sekunda, minuta, hodina, den, týden, měsíc, rok; značíme t

                                        rychlost - m/s nebo km/h; značíme v; rychlost auta-potřebujeme znát vzdálenost a čas

PŘEVODY - 1m=10dm=100cm=1000mm; 1mm=0,1cm=0,01dm=0,001m; 1km = 1000m

                     čtvereční se posouvají o dvě místa - 1m=100dm=10000cm=1 000 000mm; krychlové o tři místa

OBSAH A OBVOD - obsah je plocha, která je ve vnitř (vymalování pokoje), obvod co je okolo (stavění plotu okolo zahrady).

                               obsah jsme si již řekli, že vychází ve čtverečních jednotkách (na druhou)=musíme násobit dvě velikosti.

                                obvod vychází v základní jednotce metr = pouze sčítáme délky.

ČTVEREC - S= a ° a (strana na druhou) o=a+a+a+a=4 ° a

OBDÉLNÍK - S= a ° b (strana ° druhá strana) o= a+b+c+d (strany a,c jsou stejné + strany b,d jsou také stejné)=2a+2b=2(a+b).

ÚHEL - dvě polopřímky, když se protnou, tak spolu svírají úhel; měří se úhloměrem;základní jednotka je stupeň a jeden stupeň

              má 60 minut;ostrý < 90 stup.;pravý=90stup.;tupý>90 st.; přímý=180 stup.;úhly můžeme sčítat i odčítat

DĚLITELNOST - pravidla jak poznáme, že číslo je dělitelné právě tímto číslem:

         dělitelné dvěmi: na konci čísla je sudé číslo (0,3,4,6,8,) př. 134;111118;06

         dělitelné třemi: jednotlivá čísla sečteme a výsledek je dělitelný třemi. př.141=1+4+1=6/6 lze;12345=1+2+3+4+5=15/3 lze

        dělitelné čtyřmi: pokud poslední dvojčíslí jě dělitelné čtyřmi. př. 612, 1048

        dělitelnost pěti: na posledním místě je 0 nebo 5. př. 100, 2345

        dělitelnost šesti: je-li dělitelné dvěmi i třemi

         dělitelnost sedmi: že se první až posldní číslice od zadu vynásobí postupně čísly (periodicky se opakujícími): 1, 3, 2, 6, 4, 5

                                    př. 138309241 : 1*1+4*3+2*2+9*6+0*4+3*5+8*1+3*3+1*2=105 (1*5+3*0+2*1=7, číslo dělitelné 7)

         dělitelnost osmi: je-li poslední trojčíslý dělitelné osmi. př. 12016, 6064

          dělitelsnost devíti: jednotlivá čísla sečteme a výsledek je dělitelný devíti. př. 15786=1+5+7+8+6=27/9 lze

          dělitelnost desíti: končí-li číslo na nulu. př. 100, 1230, 1836400

 ARITMETICKÝ PRŮMĚR - se vypočítá sečtením všech položek a vydělením počtem položek. př. 5 a 7;(5+7)/2=12/2=6

PŘEVOD ZLOMKU NA CELKY - vydělíme čitatele jmenovatelem - vyjde celek a zbytek napíšeme do čitatele. př.15/8=1a7/8

PRVOČÍSLO - číslokteré je dělitelné pouze číslem jedna a sebou samým;př.3, 5, 7, 11, 13, 17, 22, 31;pozor číslo 1 není prvočíslo.

ROZKLAD ČÍSEL NA PRVOČÍSLA - danné číslo rozložíme na co nejmenší násobky - prvočísla. př. 27=9 ° 3=3°3°3

NEJMENŠÍ SPOLEČNÝ NÁSOBEK - nalézneme tak, že každé z čísel je rozložíme na součin prvočísel a yvpíšme čísla, která se

                                                                   vyskytují alespoň v jednom rozkladu; př. čísla: 15 a 20

                                                                    1. Číslo 15 lze rozložit na součin prvočísel 3 × 5

                                                                    2. Číslo 20 lze rozložit na součin 2 × 2 × 5

                                                                    3. Nejmenší součin musí obsahovat 2 × 2 × 3 × 5, což je 60.

                                                                   př.   Zadaná čísla: 15, 20, 90

                                                                   15 = 3 × 5,  20 = 2 × 2 × 5,  90 = 2 × 3 × 3 × 5 ----------  = 2 × 2 × 3 × 3 × 5 = 180

SPOLEČNÝ DĚLITEL - je největší číslo, které beze zbytku dělí obě čísla, tzn. největší číslo, jímž jsou obě čísla dělitelná;

                                           př. společný dělitel čísel 15 a 20 je 5 (číslo 5 dělí obě čísla)= 15/5=lze, 20/5= lze

                                                žádné větší číslo s touto vlastností už neexistuje; např. číslo 10 dělí druhé číslo, ale ne první

 

 ABSOLUTNÍ HODNOTA - je to závorka / / která převádí záporné čísla na kladné (z mínus 3 se stane plus 3). př. /-3+5-8/=/-6/=6

PROCENTA % - vyjadřují část celku. Vypočítání procent z čísel: část celku / celek ° 100 = %; 2 ze 4 = 2/4°100=50%

                                                     Vypočítání části celku z procent: celek / 100 ° procenta = část celku; 50% ze 4 = 4/100°50=2

                                        Vypočítání celku z procent a části celku: 100% / počet procent °část celku = celek; 2 je 50% = 100/50°2=4

JEDNODUCHÉ ROVNICE - rovnice poznáme tak, že má rovnítko (=) takže má pravou stranu (před rovnítkem) a levou stranu (za

                                                  rovnítkem). Nejdůležitější je si uvědomit, že obě strany se musejí rovnat (musí být stejný výsledek).

                                                  př. c - 230 = 50; pokavaď je na pravé straně 50, tak na levé musí vyjít také 50. Nyní je příklad již

                                                   jednoduchý, stačí najít jen číslo za c aby vyšlo 50. Což je 280 - 230 = 50

ROVNICE - Popsali jsme si řešení jednoduchých rovnic, nyní se vrhnem na základní pravidla:

                                                                                 a) zbavíme se jmenovatelů;

                                                                                   b) zbavíme se závorek;

                                                                                   c) čísla dáme na jednu stranu rovnice a neznámé na druhou;

                                                                                  d) vždy vypočítáme kolik je 1 ° neznámá (nezajímá nás kolik je 3x, ale kolik je 1x

                   Postupujeme ekvivalentními úpravami= ekvivalentní (nezmění řešení) pravidla:

                     

                    1) Na každou stranu můžeme přičíst či odečíst stejné číslo.  ZJEDNODUŠENĚ MŮŽEME ŘÍCI, ŽE KDYŽ PŘENÁŠÍME

                        JEDNO ČÍSLO NA DRUHOU STRANU ROVNICE MĚNÍME ZNAMÉNKO (opak sčítání je odčítání):               

                                                                                                    

                                                          př. c - 230 = 50 (na obě strany přičteme 230 abysme se zbavily 230 na levé straně);

                                                                c - 230 + 230 = 50 + 230 (nyní nám na levé straně zůstane jen c, jelikož -230+230=0);

                                                                c = 50 + 230;                       c = 280

                             ZJEDNODUŠENĚ: c - 230 = 50; c = 50 + 230; c = 280 (číslo jsme daly na druhou stranu a jen změnily znaménko)

                     2) Každou stranu můžeme vynásobit či vydělit stejným číslem. ZJEDNODUŠENĚ MŮŽEME ŘÍCI, ŽE KDYŽ

                          PŘENÁŠÍME NÁSOBEK NA DRUHOU STRANU ROVNICE UDĚLÁME Z NĚJ DĚLITELE A NAOPAK 

                          (opak násobení je dělení):

                                                           př. 2c - 230 = 50 (čísla dáme na jednu stranu a neznámou na druhou stranu, popsali jsme výše) 

                                                                2c = 50 + 230;                       2c = 280

                                                                2c/2 = 280/2 (celou rovnici vydělíme dvěma, abychom dostali 1c);

                                                                  c = 280/2 (2c/2 = 1c , dvojky se vykrátí);                       c=140

                       ZJEDNODUŠENĚ: 2c = 280; c=280/2 (násobek neznámé c (2) jsme přenesli na druhou stranu a stal se z něj dělitel)

 

 

           

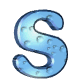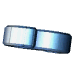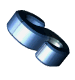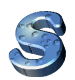
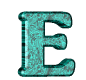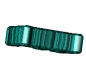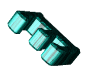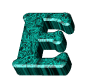
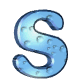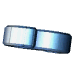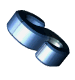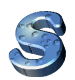
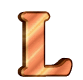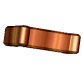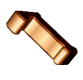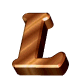
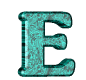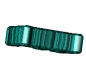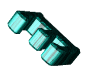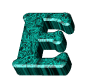
 je jednička,   je dvojka,  je trojka,  je čtyřka,  je pětka,

 je ěestka,  je sedmička, je osmička,

 je devítka,  je desítka, ...,  je padesátka,  je stovka,  je pětset,  je tisíc

 

př. 1988 je